
Under the condition:
S = distance covered (km, m)V = speed (km / h, m / s)T= travel time (hour, second)Note:
To find a distance, the formula is
 .
. To search for travel time, the formula is
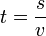 .
.To search for speed, the formula is
 Average speedFormula:
Average speedFormula:
Uniformly accelerated motionUniformly accelerated motion is a motion trajectory is a straight line with a speed that is changed irregularly.The acceleration is constant / fixed.The formula uniformly accelerated motion there are three, namely:
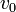 =The initial velocity (m/s)
=The initial velocity (m/s) =final speed(m/s)
=final speed(m/s)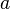 = Acceleration (m/s2)
= Acceleration (m/s2) =distance covered (m)
=distance covered (m)
Vertical movement upwardsObject thrown vertically, perpendicular to the horizontal plane upwards with a certain initial velocity. The direction of motion of the object and the opposite direction of the gravitational acceleration, uniformly accelerated motion is slowed.Bullets will reach its highest point when Vt equal to zero.
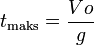

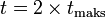

Description:
Initial velocity = Vo
Velocity at a certain height = Vt
Acceleration / Gravity earth: g
Maximum height: h
Time object reached its highest point: t max
The time when the object back to the ground: t Motion free fallObject when the object is said to be in free fall:
Has a certain height (h) above the ground.
The object is dropped perpendicular to the horizontal plane without initial velocity.During moves down, the object is affected by the Earth's gravitational acceleration (g) and the direction of the speed / direction of motion of a body, a uniformly accelerated motion accelerated.
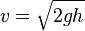
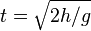
Description:
v = velocity at ground level
g = gravity of the earth
h = height from ground level
t = old objects to the ground Vertical motion downwardsObjects thrown in his direction perpendicular to the horizontal plane down.Direction of the gravitational acceleration and direction of movement of the direction, a uniformly accelerated motion accelerated.


Description:
Vo = initial speed
Vt = speed at a certain height from the ground
g = gravity of the earth
h = distance traveled vertically
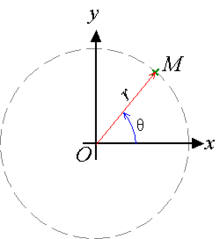
t = time Circular motionMotion with the trajectory of a circle.
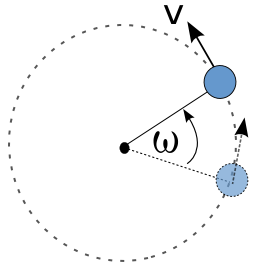 Circular motion diagram.pngFrom the diagram above, the moving object is known so far ω ° for t seconds, then the body is said to shift the angle.Objects put through one full rotation. Large linear displacement is 2 \ pi r or the circumference of a circle. Large angular displacement in one full rotation is 2 \ pi radians or 360 °.
Circular motion diagram.pngFrom the diagram above, the moving object is known so far ω ° for t seconds, then the body is said to shift the angle.Objects put through one full rotation. Large linear displacement is 2 \ pi r or the circumference of a circle. Large angular displacement in one full rotation is 2 \ pi radians or 360 °.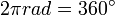

Angular displacement, angular velocity and angular accelerationThe angular displacement is the angular position of objects moving in a circle within a certain time interval.
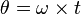
Description:
 = displacement angle (rad)
= displacement angle (rad)w = angular velocity (rad / s)
t = time (second)The average angular velocity (\ overline {\ omega}): the angular displacement per interval.

The average angular acceleration (\ alpha): angular velocity changes per interval.

 : Acceleration angle (rad / s2) Centripetal accelerationDirection of the centripetal acceleration is always toward the center of the circle.Centripetal acceleration does not pick up speed, but just to keep things in order to keep moving in a circle.
: Acceleration angle (rad / s2) Centripetal accelerationDirection of the centripetal acceleration is always toward the center of the circle.Centripetal acceleration does not pick up speed, but just to keep things in order to keep moving in a circle.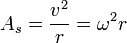
Description:
r: radius of the object / circle
As: the centripetal acceleration (rad / s2)
Parabolic motionParabolic motion is a motion that forms a certain angle to the horizontal plane. In the parabolic motion, friction is negligible, and the forces acting only gravity / acceleration due to gravity.
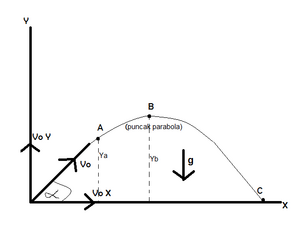
Motion parabola.pngAt the starting point,


At point A (t = ta):

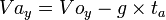
Location / position in A:


The highest attainable point (B):
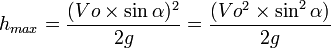
Time to reach the highest point (B) (tb):
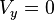

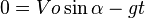

The distance horizontally / horizontally from the starting point to point B (Xb):
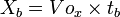
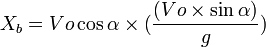

The vertical distance from the starting point to point B (Yb):


The time to reach point C:
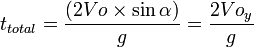
The distance from the initial ball moves to point C:

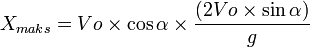
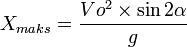
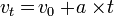

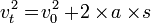
Tidak ada komentar:
Posting Komentar